안녕하세요. 이번에는 백준 9059 1, 2, 3 더하기 문제를 풀어보려고 합니다.
https://www.acmicpc.net/problem/9095
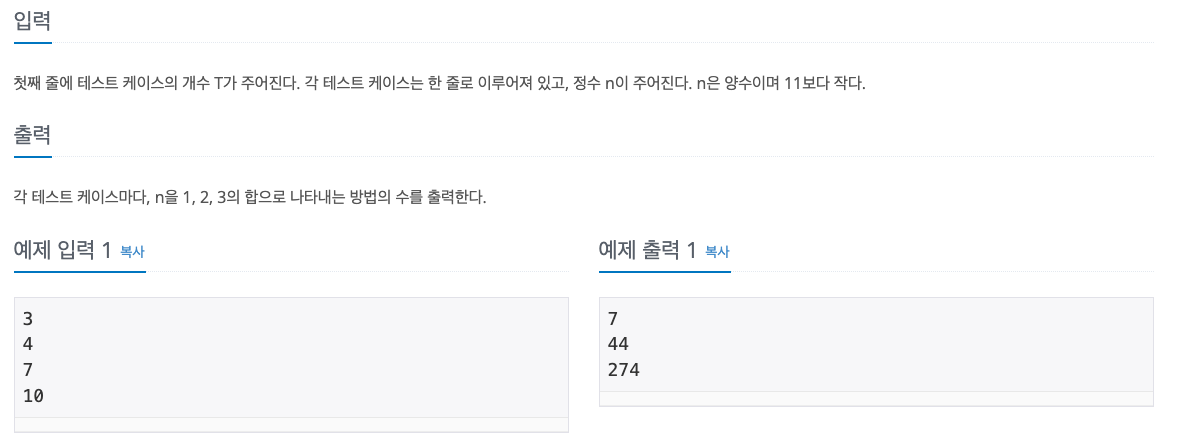
9095번: 1, 2, 3 더하기
각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 출력한다.
www.acmicpc.net
Problem
정수 4를 1, 2, 3의 합으로 나타내는 방법은 총 7가지가 있다. 합을 나타낼 때는 수를 1개 이상 사용해야 한다.
- 1+1+1+1
- 1+1+2
- 1+2+1
- 2+1+1
- 2+2
- 1+3
- 3+1
정수 n이 주어졌을 때, n을 1, 2, 3의 합으로 나타내는 방법의 수를 구하는 프로그램을 작성하시오.
Solution
import java.io.*;
import java.util.*;
public class Main {
static int[] dp = new int[12];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int T = Integer.parseInt(br.readLine());
makeDp();
for(int i = 0; i < T; i++) {
int num = Integer.parseInt(br.readLine());
sb.append(dp[num]).append("\n");
}
System.out.println(sb.toString());
}
static void makeDp() {
dp[0] = 0;
dp[1] = 1;
dp[2] = 2;
dp[3] = 4;
for(int i = 4; i < 12; i++) {
dp[i] = dp[i - 3] + dp[i - 2] + dp[i - 1];
}
}
}이번 문제는 1, 2, 3을 이용하여 n을 나타내는 방법의 수를 구하는 문제이다.
1, 2, 3을 만드는 경우의 수
1 = 1 > 1번
2 = 1 + 1 , 2 > 2번
3 = 1 + 1 + 1, 1 + 2, 2 + 1, 3 > 4번
4 = 1에 + 3, 2에 + 2, 3에 + 1을 하는 경우의 수이다.
5 = 2에 + 3, 3에 + 2, 4에 + 1을 하는 경우의 수가 있다.
이것을 점화식으로 표현하면, dp[n] = dp[n - 3] + dp[n - 2] + dp[n - 1]을 만들 수 있다.
1. 핵심 코드 : dp[n] = dp[n - 3] + dp[n - 2] + dp[n - 1] 점화식
static void makeDp() {
dp[0] = 0;
dp[1] = 1;
dp[2] = 2;
dp[3] = 4;
for(int i = 4; i < 12; i++) {
dp[i] = dp[i - 3] + dp[i - 2] + dp[i - 1];
}
}Performance

반응형
'백준 Algorithm > 백준 CLASS3' 카테고리의 다른 글
| [백준] CLASS3 11659 구간 합 구하기4 - JAVA [자바] (0) | 2023.10.31 |
|---|---|
| [백준] CLASS3 11399 ATM - JAVA [자바] (0) | 2023.10.30 |
| [백준] CLASS3 7576 토마토 - JAVA [자바] (0) | 2023.10.28 |
| [백준] CLASS3 2630 색종이 만들기 - JAVA [자바] (0) | 2023.10.27 |
| [백준] CLASS3 2606 바이러스 - JAVA [자바] (0) | 2023.10.26 |



